Substituting for x and t from the above Lorentz transformations one obtains
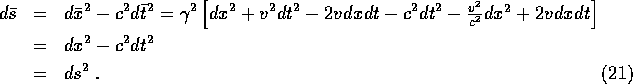
Generalizing to four dimensions we see that the spacetime interval
is invariant under the Lorentz transformations.
The most general transformation between 
and 
will be more complicated but it must be linear. We can write it
as:
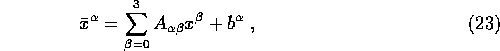
where 
. This linear
transformation is called the generalized Lorentz transformations.
It contains ten parameters:
four correspond to an origin shift 
, three
correspond to a Lorentz boost [ which depends on 
]
and three to the rotation which aligns the axes of
and . The last six are contained in the 
matrix 
[ six because is symmetric
i.e. 
.
Later we will show that the Poincaré transformations
preserve Maxwells equations as well as light paths.